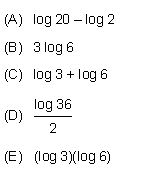|
VESTIBULAR UFF/1997 Matemática - 1ª Etapa |
|---|
 |
VESTIBULAR UFF/1997 Matemática - 1ª Etapa |
|---|
01 A razão entre o lado do quadrado inscrito e o lado do quadrado circunscrito em uma circunferência de raio R é:
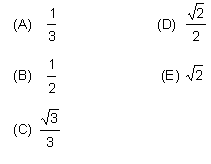
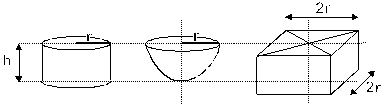
02 Na figura estão representados três sólidos de mesma altura h — um cilindro, uma semi-esfera e um prisma — cujos volumes são
![]() , respectivamente.
, respectivamente.

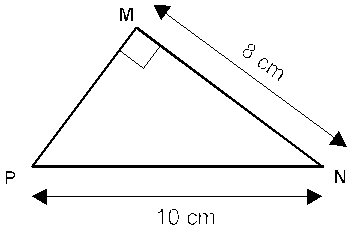
03 Considere o triângulo PMN, retângulo em M, representado na figura abaixo.
(A) 4
(B) 6
(C) 12
(D) 20
(E) 24
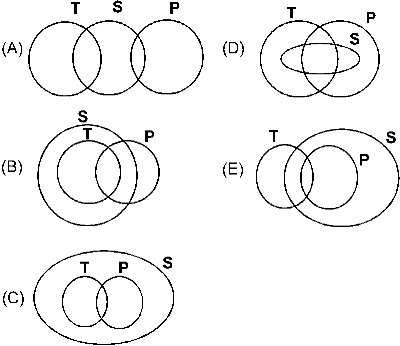
04 Os conjuntos S, T e P são tais que todo elemento de S é elemento de T ou P.
05 As equações
![]() representam no plano, respectivamente:
representam no plano, respectivamente:
(A) uma reta, uma hipérbole e uma parábola
(B) uma parábola, uma hipérbole e uma reta
(C) uma reta, uma parábola e uma elipse
(D) uma elipse, uma parábola e uma hipérbole
(E) umareta, uma parábola e uma hipérbole
06 Toda matriz de ordem 2 x 2, que é igual a sua transposta, possui:
(A) pelos menos dois elementos iguais
(B) os elementos da diagonal principal iguais a zero
(C) determinante nulo
(D) linhas proporcionais
(E) todos os elementos iguais a zero
07 A equação da parábola que passa pelo ponto (– 2,0) e cujo vértice situa-se no ponto (1,3) é:
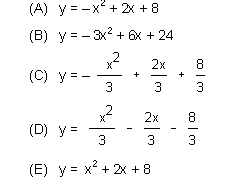
08 Um prédio com a forma de um paralelepípedo retângulo tem 48 m de altura. No centro da cobertura desse prédio e perpendicularmente a essa cobertura, está instalado um pára-raios. No ponto Q sobre a reta r — que passa pelo centro da base do prédio e é perpendicular a
![]() - está um observador que avista somente uma parte do pára-raios (ver a figura).
- está um observador que avista somente uma parte do pára-raios (ver a figura).
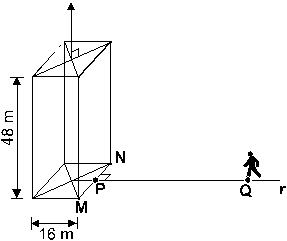
(A) 16 m
(B) 12 m
(C) 8 m
(D) 6 m
(E) 3 m
09 Considere os seguintes enunciados:
(A) se 15 é múltiplo de 7 ou 16 é múltiplo de 2 então 8 é número primo.
(B) se 16 é múltiplo de 2 ou 8 é número primo então 15 é múltiplo de 7.
(C) se 16 é múltiplo de 2 então 15 é múltiplo de 7 e 8 é número primo.
(D) se 15 é múltiplo de 7 e 8 é número primo então 16 é múltiplo de 2.
(E) se 16 é múltiplo de 2 então 15 é múltiplo de 7 ou 8 é número primo.
10 Marque a opção que indica quantos pares de retas reversas são formados pelas retas suportes das arestas de um tetraedro.
(A) Um par.
(B) Dois pares.
(C) Três pares.
(D) Quatro pares.
(E) Cinco pares.
11 Dados ![]() tais que
tais que
![]() , considere as afirmativas:
, considere as afirmativas:
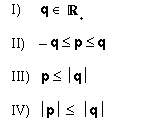
(A) somente a I e a II.
(B) somente a I e a III.
(C) somente a II e a III.
(D) somente a I , a II e a III.
(E) todas as afirmativas.
12 Considere as funções f, g e h, todas definidas em [m, n] com imagens em [p, q] representadas através dos gráficos abaixo:
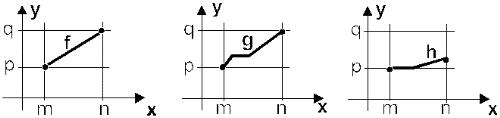
(A) f é bijetiva, g é sobrejetiva e h não é injetiva.
(B) f é sobrejetiva, g é injetiva e h não é sobrejetiva.
(C) f não é injetiva, g é bijetiva e h é injetiva.
(D) f é injetiva, g não é sobrejetiva e h é bijetiva.
(E) f é sobrejetiva, g não é injetiva e h é sobrejetiva.
13 Com as letras da palavra PROVA podem ser escritos x anagramas que começam por vogal e y anagramas que começam e terminam por consoante.
(A) 48 e 36
(B) 48 e 72
(C) 72 e 36
(D) 24 e 36
(E) 72 e 24
14 Considere os números complexos m, n, p e q, vértices de um quadrado com lados paralelos aos eixos e centro na origem, conforme a figura abaixo.
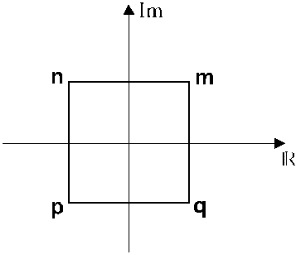
(A) é um real não nulo.
(B) é igual a zero.
(C) possui módulo unitário.
(D) é um imaginário puro.
(E) é igual a 1 + i.
15 A figura abaixo, representa duas circunferências C e C' de mesmo raio r.
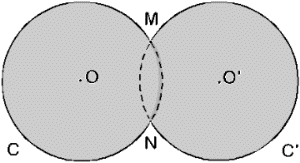
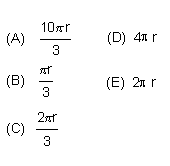
16 O triângulo MNP é tal que
![]() .
.
(A) 20º
(B) 30º
(C) 40º
(D) 50º
(E) 60º
17 Na eleição para prefeito de um município concorreram os candidatos X e Y.
(A) 47,5% para X, 44% para Y, 6,5% nulos e 2% em branco.
(B) 9,5% para X, 63% para Y, 25,5% nulos e 2 % em branco.
(C) 46% para X, 43% para Y, 8% nulos e 3% em branco.
(D) 42% para X, 44% para Y, 12% nulos e 2% em branco.
(E) 6,2% para X, 18,8% para Y, 25% nulos e 50% em branco.
18 Para ![]() , conclui-se que:
, conclui-se que:

19 Sendo x um número real não nulo, a soma do 3º termo da Progressão Aritmética (x, 2x, ...) com o 3º termo da Progressão Geométrica (x, 2x, ...) é igual a:
(A) 4x
(B) 5x
(C) 6x
(D) 7x
(E) 8x
20 Pode-se afirmar que o valor de log 18 é igual a: